DB의 성능
DB는 많은 사람들이 공통으로 사용하는 데이터 모음이기 때문에, 대량의 데이터가 조회/저장되는 일이 빈번하게 발생한다.
그리고 이를 빠르게 진행하는 것이 무엇보다 중요하다. 이때 DB의 성능과 관련된 핵심이 디스크 I/O를 어떻게 줄이느냐이다.
디스크 I/O = 플래터(원판)을 돌리고, 디스크 헤더를 이동하여 데이터를 읽는 것을 의미한다.
물론 순차 I/O가 랜덤 I/O보다 빠르다. 하지만 현실은 대부분 랜덤 I/O이며, 이를 순차로 바꾸어 보자는 아이디어에서 Index와 쿼리 튜닝이 나타났다.

Index란?
Index란 추가적인 저장 공간을 활용하여 DB 테이블의 검색 속도를 향상시키기 위한 자료구조이다.
만약 DB 테이블의 모든 데이터를 검색해서 원하는 결과를 가져오려면 시간이 오래 걸릴 것이다. 이를 해결하기 위해서 칼럼 값과 해당 레코드의 주소를 가진 인덱스를 만들어 데이터 탐색을 빠르게 하는 것이다.

이는 조회(Select)외 에도 조건문이 있는 Update나 Delete의 성능에도 영향을 준다.
// Mang이라는 이름을 업데이트 해주기 위해서는 Mang을 조회해야 한다.
UPDATE USER SET NAME = 'MangKyu' WHERE NAME = 'Mang';
Index는 빠른 탐색을 지원하기 위해 항상 정렬된 상태를 유지한다. 따라서 INSERT, UPDATE, DELETE에서 추가적인 연산이 필요하다.
이를 간단히 정리하자면 아래와 같다.
😀 장점
- 테이블을 조회하는 속도와 성능 향상
- 시스템 부하를 줄임
😫 단점
- 인덱스를 관리하기 위한 추가 저장 공간 필요
- 인덱스를 항상 정렬된 상태로 유지하기에 추가 작업이 필요
- 인덱스를 잘못 사용할 경우 역효과가 날 수 있음
🤔 Index 권장 케이스
- 데이터 양이 많은 테이블
- 업데이트보다 조회가 잦은 테이블
- 조건문이나 정렬이 잦은 테이블
Index 자료구조
1. Hash 인덱스 알고리즘 | O(1)
해시 값을 계산해서 인덱싱하는 알고리즘으로 매우 빠른 검색(O(1))을 지원한다.
이는 등호 연산(=)에는 적절하나, 값을 변현해서 사용하기 때문에 부등호 연산(>, <), 값의 일부를 검색(like ‘A*’)에 부적절하다.

2. B+-Tree 인덱스 알고리즘 | O(logN)
일반적으로 사용되는 인덱스 알고리즘이다. 값을 변형하지 않고, 원래 값을 이용한다.
👉 B-Tree
Binary Search Tree와 유사하다. 다른 점은 자식 노드를 2개 이상 가질 수 있고, 균형트리다. 따라서 비균형 트리가 될 때 균형을 맞출 필요가 있고, 추가적인 연산이 필요하다.
이는 Root Node / Branch Node / Leaf Node로 나뉜다.
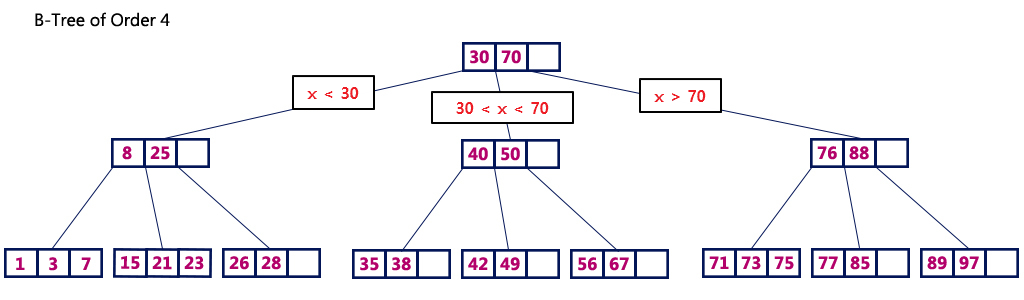
👉 B+ Tree
B-Tree의 확장 개념이다. 오직 리프 노드만 인덱스-값을 가지고 있고, Linked List로 연결되어 있다.
이는 한 노드에 많은 key를 담을 수 있어 트리의 높이가 낮아진다.
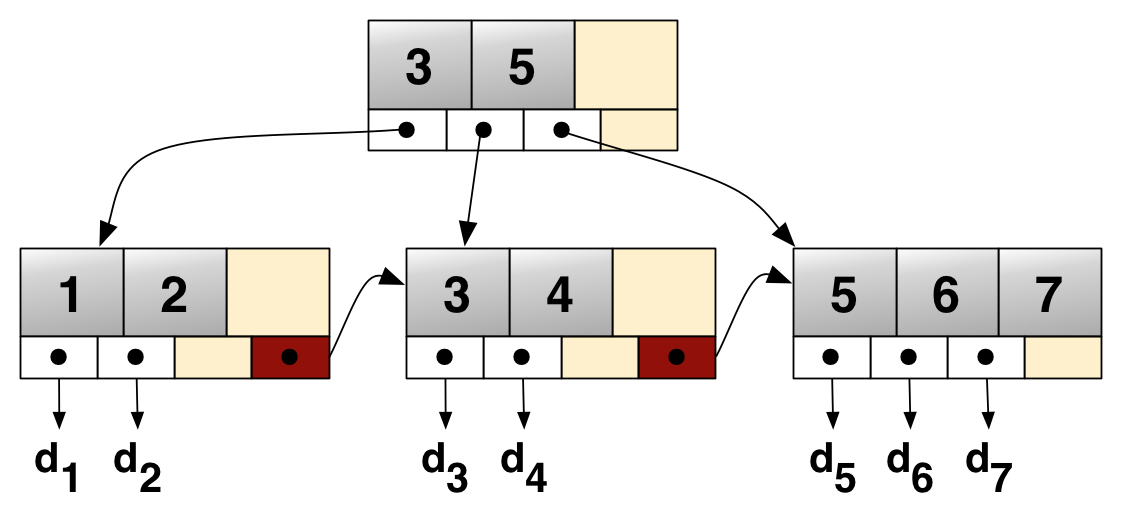
참고
https://zorba91.tistory.com/293
https://mangkyu.tistory.com/96
'Engineering 💻 > DB' 카테고리의 다른 글
| [MongoDB] Timezone(타임존) 문제와 해결 (feat.Python) (0) | 2022.02.19 |
|---|---|
| [PostgreSQL] Python에서 다중 행을 Insert하는 다양한 방법과 비교 (0) | 2022.02.10 |
| [DB] 데이터베이스 기초 (0) | 2022.01.10 |
